Mie Scattering
R. Checa-Garcia (CC BY-NC-SA) SCIENCE-BLOG
Radiative Theory Atmospheric Physics
Notebook
Post under construction
Definition: Mie Scattering is a solution of the scattering problem described with the Maxwell Equations when the scatter is a spherical particle. Initially the solution of Mie (or Lorenz-Mie) was designed for homogeneous spheres, however there are extensions for multi-layered spheres and with important limitations for other geometrical objects. The calculation is relatively efficient but depends on the size parameter, \(x=2\pi r/\lambda\). When this parameter increases the number of terms of the series necessaries to calculate the relevant amounts also grows.
The Scattering problem
The scattering problem can be formulated within the Maxwell Theory as, \[\vec{E}_{s}=f(R)\mathbf{S}(\Omega)\vec{E}_{i}\]
where \(\vec{E}_{s}\) its the scattered electric field vector and \(\vec{E}_{i}\) its the incident electric field. \(\mathbf{S}(\Omega)\) is the scattering matrix (a 2x2 matrix). We have indicated a dependence on solid angle \(\Omega\). In the case of isotropic spheres the dependency its only \(\vec{k}_{i}\cdot \vec{k}_{s}=cos(\theta)\). And \(f(R)\) it is just a function of the distance (we are usually in far field approximation). In general the scattering matrix its a complex matrix.
For spheres (and probably also for any set of scatters with randomly oriented axis) the scattering matrix is diagonal.
The Phase Matrix
In the Atmospheric Radiation studies it is quite common use the Stokes vector, so we have an incident stokes vector \(\vec{I}_{i}\) and an scattered stokes vector \(\vec{I}_{s}\) and the scattering problem is written as1, \[\vec{I}_{s}=h(R)\mathbf{F}(\Omega)\vec{I}_{i}\]
here \(\mathbf{F}(\Omega)\) its a 4x4 real matrix called Transformation Matrix \[\begin{bmatrix} F_{11}(\theta) & F_{12}(\theta) & 0 & 0 \\ F_{21}(\theta) & F_{22}(\theta) & 0 & 0 \\ 0 & 0 & F_{33}(\theta) & F_{34}(\theta) \\ 0 & 0 & F_{43}(\theta) & F_{44}(\theta) \end{bmatrix}\]
while the Phase Matrix is the transformation matrix with a factor proportional to the scattering cross-section that we will introduce later. Both formulations of the problem are equivalent as the real elements of the Phase Matrix can be estimated from the complex elements of the scattering matrix, in fact theMie Scattering theory gives us a method to calculate the scattering matrix.
The scattering matrix can be written as, \[\begin{bmatrix} S_{1}(\theta) & 0 \\ 0 & S_{2}(\theta) \end{bmatrix}\]
with \[S_{1}(\theta) = \sum_{n=1}^{N_{max}}\frac{2n+1}{n(n+1)}\left[ a_{n}\pi_{n}(\theta)+b_{n}\tau_{n}(\theta) \right]\] \[S_{2}(\theta) = \sum_{n=1}^{N_{max}}\frac{2n+1}{n(n+1)}\left[ b_{n}\pi_{n}(\theta)+a_{n}\tau_{n}(\theta) \right]\]
The series of values \(A_{Nmax}=\{a_{n}, \, n=1, N_{max}\}\), \(B_{Nmax}=\{b_{n}, \, n=1, N_{max}\}\), are estimated from spherical Bessel functions.
These series are used directly to calculate the Efficiency Factor of Extinction, scattering and absorption. But also the single albedo, or the asymmetry factor.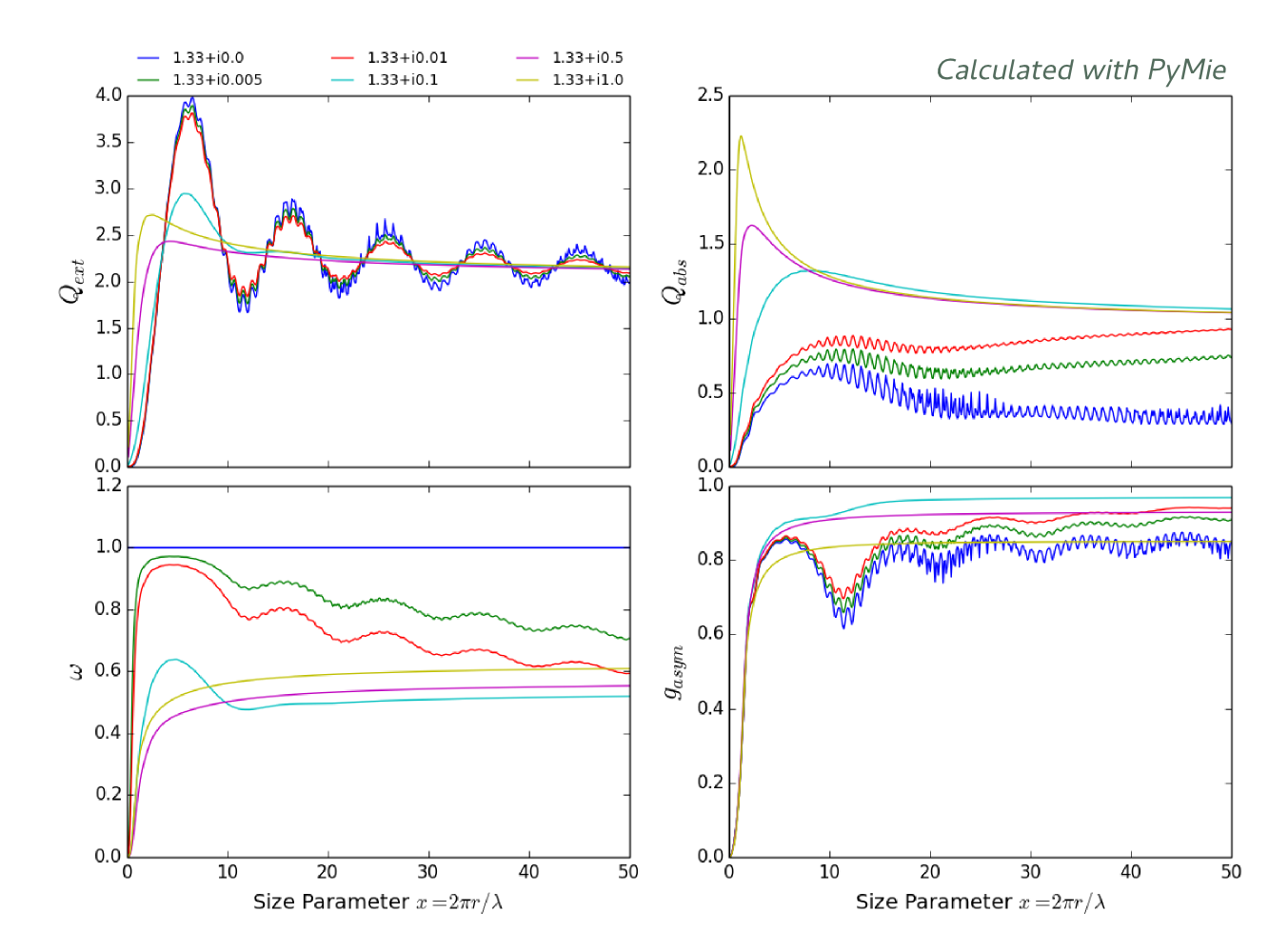
Note: The called T-matrix formalism it is an efficient alternative to Mie-Scattering. In particular, the T-matrix formalism is quite convinient for raindrop studies because the estimation of the scattering properties of Oblate Spheroid and Chebyshev particles is relatively easy described. The idea behind the theory is appealing: (1). The incident and scattered electric fields are expresed as a sum of spherical functions whose coeficientes, before and after the scattering process, might be related by a linear expression involving a transition matrix or T-matrix. (2). By using numerical or analytical methods expressions of this transition matrix are calculated and based on the transition matrix the optical properties estimated.
Hansen, J.E., and L.D. Travis, 1974: Light scattering in planetary atmospheres. Space Sci. Rev., 16, 527-610, doi:10.1007/BF00168069. ↩